|
|
| StateNumDiffTpl (std::shared_ptr< Base > state) |
| |
|
template<typename NewScalar > |
| StateNumDiffTpl< NewScalar > | cast () const |
| |
| virtual void | diff (const Eigen::Ref< const VectorXs > &x0, const Eigen::Ref< const VectorXs > &x1, Eigen::Ref< VectorXs > dxout) const override |
| | Compute the state manifold differentiation.
|
| |
|
const Scalar | get_disturbance () const |
| | Return the disturbance constant used in the numerical differentiation routine.
|
| |
| virtual void | integrate (const Eigen::Ref< const VectorXs > &x, const Eigen::Ref< const VectorXs > &dx, Eigen::Ref< VectorXs > xout) const override |
| | Compute the state manifold integration.
|
| |
| virtual void | Jdiff (const Eigen::Ref< const VectorXs > &x0, const Eigen::Ref< const VectorXs > &x1, Eigen::Ref< MatrixXs > Jfirst, Eigen::Ref< MatrixXs > Jsecond, Jcomponent firstsecond=both) const override |
| | This computes the Jacobian of the diff method by finite differentiation:
|
| |
| virtual void | Jintegrate (const Eigen::Ref< const VectorXs > &x, const Eigen::Ref< const VectorXs > &dx, Eigen::Ref< MatrixXs > Jfirst, Eigen::Ref< MatrixXs > Jsecond, const Jcomponent firstsecond=both, const AssignmentOp op=setto) const override |
| | This computes the Jacobian of the integrate method by finite differentiation:
|
| |
| virtual void | JintegrateTransport (const Eigen::Ref< const VectorXs > &x, const Eigen::Ref< const VectorXs > &dx, Eigen::Ref< MatrixXs > Jin, const Jcomponent firstsecond=both) const override |
| | Parallel transport from integrate(x, dx) to x.
|
| |
| virtual void | print (std::ostream &os) const override |
| | Print relevant information of the state numdiff.
|
| |
| virtual VectorXs | rand () const override |
| | Generate a random state.
|
| |
|
void | set_disturbance (const Scalar disturbance) |
| | Modify the disturbance constant used by the numerical differentiation routine.
|
| |
| virtual VectorXs | zero () const override |
| | Generate a zero state.
|
| |
| | StateAbstractTpl (const std::size_t nx, const std::size_t ndx) |
| | Initialize the state dimensions.
|
| |
| VectorXs | diff_dx (const Eigen::Ref< const VectorXs > &x0, const Eigen::Ref< const VectorXs > &x1) |
| | Compute the state manifold differentiation.
|
| |
|
bool | get_has_limits () const |
| | Indicate if the state has defined limits.
|
| |
|
const VectorXs & | get_lb () const |
| | Return the state lower bound.
|
| |
|
std::size_t | get_ndx () const |
| | Return the dimension of the tangent space of the state manifold.
|
| |
|
std::size_t | get_nq () const |
| | Return the dimension of the configuration tuple.
|
| |
|
std::size_t | get_nv () const |
| | Return the dimension of tangent space of the configuration manifold.
|
| |
|
std::size_t | get_nx () const |
| | Return the dimension of the state tuple.
|
| |
|
const VectorXs & | get_ub () const |
| | Return the state upper bound.
|
| |
| VectorXs | integrate_x (const Eigen::Ref< const VectorXs > &x, const Eigen::Ref< const VectorXs > &dx) |
| | Compute the state manifold integration.
|
| |
| std::vector< MatrixXs > | Jdiff_Js (const Eigen::Ref< const VectorXs > &x0, const Eigen::Ref< const VectorXs > &x1, const Jcomponent firstsecond=both) |
| |
| std::vector< MatrixXs > | Jintegrate_Js (const Eigen::Ref< const VectorXs > &x, const Eigen::Ref< const VectorXs > &dx, const Jcomponent firstsecond=both) |
| | Compute the Jacobian of the state manifold integration.
|
| |
|
void | set_lb (const VectorXs &lb) |
| | Modify the state lower bound.
|
| |
|
void | set_ub (const VectorXs &ub) |
| | Modify the state upper bound.
|
| |
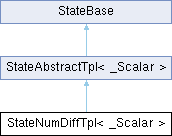
template<typename _Scalar>
class crocoddyl::StateNumDiffTpl< _Scalar >
Definition at line 20 of file state.hpp.
template<typename _Scalar >
| virtual void diff |
( |
const Eigen::Ref< const VectorXs > & |
x0, |
|
|
const Eigen::Ref< const VectorXs > & |
x1, |
|
|
Eigen::Ref< VectorXs > |
dxout |
|
) |
| const |
|
overridevirtual |
Compute the state manifold differentiation.
The state differentiation is defined as:
\begin{equation*}
\delta\mathbf{x} = \mathbf{x}_{1} \ominus \mathbf{x}_{0},
\end{equation*}
where \(\mathbf{x}_{1}\), \(\mathbf{x}_{0}\) are the current and previous state which lie in a manifold \(\mathcal{M}\), and \(\delta\mathbf{x} \in T_\mathbf{x} \mathcal{M}\) is the rate of change in the state in the tangent space of the manifold.
- Parameters
-
| [in] | x0 | Previous state point (size nx) |
| [in] | x1 | Current state point (size nx) |
| [out] | dxout | Difference between the current and previous state points (size ndx) |
Implements StateAbstractTpl< _Scalar >.
template<typename _Scalar >
| virtual void integrate |
( |
const Eigen::Ref< const VectorXs > & |
x, |
|
|
const Eigen::Ref< const VectorXs > & |
dx, |
|
|
Eigen::Ref< VectorXs > |
xout |
|
) |
| const |
|
overridevirtual |
Compute the state manifold integration.
The state integration is defined as:
\begin{equation*}
\mathbf{x}_{next} = \mathbf{x} \oplus \delta\mathbf{x},
\end{equation*}
where \(\mathbf{x}\), \(\mathbf{x}_{next}\) are the current and next state which lie in a manifold \(\mathcal{M}\), and \(\delta\mathbf{x}
\in T_\mathbf{x} \mathcal{M}\) is the rate of change in the state in the tangent space of the manifold.
- Parameters
-
| [in] | x | State point (size nx) |
| [in] | dx | Velocity vector (size ndx) |
| [out] | xout | Next state point (size nx) |
Implements StateAbstractTpl< _Scalar >.
template<typename _Scalar >
| virtual void Jdiff |
( |
const Eigen::Ref< const VectorXs > & |
x0, |
|
|
const Eigen::Ref< const VectorXs > & |
x1, |
|
|
Eigen::Ref< MatrixXs > |
Jfirst, |
|
|
Eigen::Ref< MatrixXs > |
Jsecond, |
|
|
Jcomponent |
firstsecond = both |
|
) |
| const |
|
overridevirtual |
This computes the Jacobian of the diff method by finite differentiation:
\begin{equation}
Jfirst[:,k] = diff(int(x_1, dx_dist), x_2) - diff(x_1, x_2)/disturbance
\end{equation}
and
\begin{equation}
Jsecond[:,k] = diff(x_1, int(x_2, dx_dist)) - diff(x_1, x_2)/disturbance
\end{equation}
- Parameters
-
| Jfirst | |
| Jsecond | |
| firstsecond | |
Implements StateAbstractTpl< _Scalar >.
template<typename _Scalar >
| virtual void Jintegrate |
( |
const Eigen::Ref< const VectorXs > & |
x, |
|
|
const Eigen::Ref< const VectorXs > & |
dx, |
|
|
Eigen::Ref< MatrixXs > |
Jfirst, |
|
|
Eigen::Ref< MatrixXs > |
Jsecond, |
|
|
const Jcomponent |
firstsecond = both, |
|
|
const AssignmentOp |
op = setto |
|
) |
| const |
|
overridevirtual |
This computes the Jacobian of the integrate method by finite differentiation:
\begin{equation}
Jfirst[:,k] = diff( int(x, d_x), int( int(x, dx_dist), dx) )/disturbance
\end{equation}
and
\begin{equation}
Jsecond[:,k] = diff( int(x, d_x), int( x, dx + dx_dist) )/disturbance
\end{equation}
- Parameters
-
| Jfirst | |
| Jsecond | |
| firstsecond | |
Implements StateAbstractTpl< _Scalar >.
Public Types inherited from StateAbstractTpl< _Scalar >
1.9.8