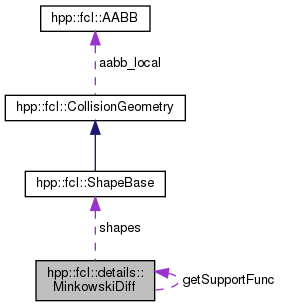
Minkowski difference class of two shapes.
More...
#include <hpp/fcl/narrowphase/gjk.h>
|
| | MinkowskiDiff () |
| |
| void | set (const ShapeBase *shape0, const ShapeBase *shape1) |
| |
| void | set (const ShapeBase *shape0, const ShapeBase *shape1, const Transform3f &tf0, const Transform3f &tf1) |
| | Set the two shapes, with a relative transformation. More...
|
| |
| Vec3f | support0 (const Vec3f &d, bool dIsNormalized) const |
| | support function for shape0 More...
|
| |
| Vec3f | support1 (const Vec3f &d, bool dIsNormalized) const |
| | support function for shape1 More...
|
| |
| void | support (const Vec3f &d, bool dIsNormalized, Vec3f &supp0, Vec3f &supp1) const |
| | support function for the pair of shapes More...
|
| |
Minkowski difference class of two shapes.
- Todo:
- template this by the two shapes. The triangle / triangle case can be easily optimized computing once the triangle shapes[1] into frame0
- Note
- The Minkowski difference is expressed in the frame of the first shape.
◆ GetSupportFunction
◆ MinkowskiDiff()
| hpp::fcl::details::MinkowskiDiff::MinkowskiDiff |
( |
| ) |
|
|
inline |
◆ set() [1/2]
| void hpp::fcl::details::MinkowskiDiff::set |
( |
const ShapeBase * |
shape0, |
|
|
const ShapeBase * |
shape1 |
|
) |
| |
Set the two shapes, assuming the relative transformation between them is identity.
◆ set() [2/2]
Set the two shapes, with a relative transformation.
◆ support()
| void hpp::fcl::details::MinkowskiDiff::support |
( |
const Vec3f & |
d, |
|
|
bool |
dIsNormalized, |
|
|
Vec3f & |
supp0, |
|
|
Vec3f & |
supp1 |
|
) |
| const |
|
inline |
support function for the pair of shapes
◆ support0()
| Vec3f hpp::fcl::details::MinkowskiDiff::support0 |
( |
const Vec3f & |
d, |
|
|
bool |
dIsNormalized |
|
) |
| const |
|
inline |
support function for shape0
◆ support1()
| Vec3f hpp::fcl::details::MinkowskiDiff::support1 |
( |
const Vec3f & |
d, |
|
|
bool |
dIsNormalized |
|
) |
| const |
|
inline |
support function for shape1
◆ getSupportFunc
◆ inflation
| Eigen::Array<FCL_REAL, 1, 2> hpp::fcl::details::MinkowskiDiff::inflation |
The radius of the sphere swepted volume. The 2 values correspond to the inflation of shape 0 and shape 1.
◆ oR1
| Matrix3f hpp::fcl::details::MinkowskiDiff::oR1 |
rotation from shape1 to shape0 such that 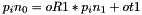 .
.
◆ ot1
| Vec3f hpp::fcl::details::MinkowskiDiff::ot1 |
translation from shape1 to shape0 such that 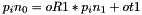 .
.
◆ shapes
| const ShapeBase* hpp::fcl::details::MinkowskiDiff::shapes[2] |
The documentation for this struct was generated from the following file:
- include/hpp/fcl/narrowphase/gjk.h
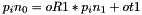 . More...
. More...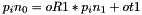 . More...
. More...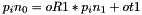 .
. 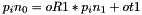 .
. 