#include <hpp/pinocchio/liegroup-space.hh>
Public Member Functions | |
| size_type | nq () const |
| Dimension of the vector representation. More... | |
| size_type | nv () const |
| Dimension of the Lie group tangent space. More... | |
| size_type | nq (const std::size_t &rank) const |
| Dimension of elementary Liegroup at given rank. More... | |
| size_type | nv (const std::size_t &rank) const |
| Dimension of elementary Liegroup tangent space at given rank. More... | |
| const std::vector< LiegroupType > & | liegroupTypes () const |
| Get reference to vector of elementary types. More... | |
| LiegroupElement | neutral () const |
| Return the neutral element as a vector. More... | |
| LiegroupElement | element (vectorIn_t q) const |
| Create a LiegroupElement from a configuration. More... | |
| LiegroupElementRef | elementRef (vectorOut_t q) const |
| Create a LiegroupElementRef from a configuration. More... | |
| LiegroupElementConstRef | elementConstRef (vectorIn_t q) const |
| Create a LiegroupElementRef from a configuration. More... | |
| LiegroupElement | exp (vectorIn_t v) const |
| Return exponential of a tangent vector. More... | |
| template<DerivativeProduct side> | |
| void | dIntegrate_dq (LiegroupElementConstRef q, vectorIn_t v, matrixOut_t Jq) const |
| template<DerivativeProduct side> | |
| void | dIntegrate_dv (LiegroupElementConstRef q, vectorIn_t v, matrixOut_t Jv) const |
| template<bool ApplyOnTheLeft> | |
| void | Jdifference (vectorIn_t q0, vectorIn_t q1, matrixOut_t J0, matrixOut_t J1) const |
| template<DerivativeProduct side> | |
| void | dDifference_dq0 (vectorIn_t q0, vectorIn_t q1, matrixOut_t J0) const |
| template<DerivativeProduct side> | |
| void | dDifference_dq1 (vectorIn_t q0, vectorIn_t q1, matrixOut_t J1) const |
| void | interpolate (vectorIn_t q0, vectorIn_t q1, value_type u, vectorOut_t result) const |
| std::string | name () const |
| Return name of Lie group. More... | |
| void | mergeVectorSpaces () |
| LiegroupSpacePtr_t | vectorSpacesMerged () const |
| bool | isVectorSpace () const |
| bool | operator== (const LiegroupSpace &other) const |
| bool | operator!= (const LiegroupSpace &other) const |
| LiegroupSpacePtr_t | operator*= (const LiegroupSpaceConstPtr_t &other) |
Static Public Member Functions | |
| static LiegroupSpacePtr_t | create (const size_type &size) |
| Create instance of vector space of given size. More... | |
| static LiegroupSpacePtr_t | createCopy (const LiegroupSpaceConstPtr_t &other) |
| Create copy. More... | |
| static LiegroupSpacePtr_t | create (const LiegroupType &type) |
| Create instance with one Elementary Lie group. More... | |
Elementary Lie groups | |
| static LiegroupSpacePtr_t | Rn (const size_type &n) |
| static LiegroupSpacePtr_t | R1 () |
Return 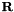 as a Lie group. More... as a Lie group. More... | |
| static LiegroupSpacePtr_t | R2 () |
Return 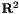 as a Lie group. More... as a Lie group. More... | |
| static LiegroupSpacePtr_t | R3 () |
Return 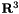 as a Lie group. More... as a Lie group. More... | |
| static LiegroupSpacePtr_t | SE2 () |
Return 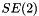 . More... . More... | |
| static LiegroupSpacePtr_t | SE3 () |
Return 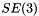 . More... . More... | |
| static LiegroupSpacePtr_t | SO2 () |
Return 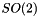 . More... . More... | |
| static LiegroupSpacePtr_t | SO3 () |
Return 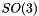 . More... . More... | |
| static LiegroupSpacePtr_t | R2xSO2 () |
Return 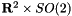 . More... . More... | |
| static LiegroupSpacePtr_t | R3xSO3 () |
Return 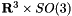 . More... . More... | |
| static LiegroupSpacePtr_t | empty () |
| Return empty Lie group. More... | |
Protected Member Functions | |
| LiegroupSpace (const size_type &size) | |
| Constructor of vector space of given size. More... | |
| LiegroupSpace (const LiegroupSpace &other) | |
| LiegroupSpace (const LiegroupType &type) | |
Detailed Description
Cartesian product of elementary Lie groups
Some values produced and manipulated by functions belong to Lie groups For instance rotations, rigid-body motions are element of Lie groups.
Elements of Lie groups are usually applied common operations, like
- integrating a velocity from a given element during unit time,
- computing the constant velocity that moves from one element to another one in unit time.
By analogy with vector spaces that are a particular type of Lie group, the above operations are implemented as operators + and - respectively acting on LiegroupElement instances.
This class represents a Lie group as the cartesian product of elementaty Lie groups. Those elementary Lie groups are gathered in a variant called LiegroupType.
Elements of a Lie group are represented by class LiegroupElement.
Constructor & Destructor Documentation
◆ LiegroupSpace() [1/3]
|
protected |
Constructor of vector space of given size.
◆ LiegroupSpace() [2/3]
|
protected |
◆ LiegroupSpace() [3/3]
|
protected |
Member Function Documentation
◆ create() [1/2]
|
inlinestatic |
Create instance of vector space of given size.
◆ create() [2/2]
|
inlinestatic |
Create instance with one Elementary Lie group.
◆ createCopy()
|
inlinestatic |
Create copy.
◆ dDifference_dq0()
| void hpp::pinocchio::LiegroupSpace::dDifference_dq0 | ( | vectorIn_t | q0, |
| vectorIn_t | q1, | ||
| matrixOut_t | J0 | ||
| ) | const |
Compute the Jacobian matrices of the difference operation. Given 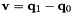 ,
,
Compute matrices 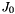 and
and 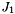 such that
such that

- Parameters
-
[in] q0,q1 Lie group elements, [out] J0 the Jacobian of v with respect to q0.
◆ dDifference_dq1()
| void hpp::pinocchio::LiegroupSpace::dDifference_dq1 | ( | vectorIn_t | q0, |
| vectorIn_t | q1, | ||
| matrixOut_t | J1 | ||
| ) | const |
Compute the Jacobian matrices of the difference operation. Given 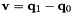 ,
,
Compute matrices 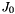 and
and 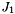 such that
such that

- Parameters
-
[in] q0,q1 Lie group elements, [out] J1 the Jacobian of v with respect to q1.
◆ dIntegrate_dq()
| void hpp::pinocchio::LiegroupSpace::dIntegrate_dq | ( | LiegroupElementConstRef | q, |
| vectorIn_t | v, | ||
| matrixOut_t | Jq | ||
| ) | const |
Compute the Jacobian of the integration operation with respect to q.
Given 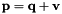 , compute
, compute 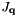 such that
such that

for constant 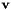
- Parameters
-
q the configuration, v the velocity vector,
- Return values
-
Jq the Jacobian (initialized as identity)
- Note
- For each elementary Lie group in q.space (), ranging over indices
![$[iq, iq+nq-1]$](form_31.png) , the Jacobian
, the Jacobian ![$J_{Lg} (q [iq:iq+nq])$](form_32.png) is computed by method pinocchio::LieGroupBase::dIntegrate_dq. lines
is computed by method pinocchio::LieGroupBase::dIntegrate_dq. lines ![$[iq:iq+nq]$](form_33.png) of Jq are then left multiplied by
of Jq are then left multiplied by ![$J_{Lg} (q [iq:iq+nq])$](form_32.png) .
.
◆ dIntegrate_dv()
| void hpp::pinocchio::LiegroupSpace::dIntegrate_dv | ( | LiegroupElementConstRef | q, |
| vectorIn_t | v, | ||
| matrixOut_t | Jv | ||
| ) | const |
Compute the Jacobian of the integration operation with respect to v.
Given 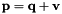 , compute
, compute 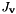 such that
such that

for constant 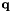
- Parameters
-
q the configuration, v the velocity vector,
- Return values
-
Jv the Jacobian (initialized to identity)
- Note
- For each elementary Lie group in q.space (), ranging over indices
![$[iv, iv+nv-1]$](form_37.png) , the Jacobian
, the Jacobian ![$J_{Lg} (q [iv:iv+nv])$](form_38.png) is computed by method pinocchio::LieGroupBase::dIntegrate_dq. lines
is computed by method pinocchio::LieGroupBase::dIntegrate_dq. lines ![$[iv:iv+nv]$](form_39.png) of Jv are then left multiplied by
of Jv are then left multiplied by ![$J_{Lg} (q [iv:iv+nv])$](form_38.png) .
.
◆ element()
| LiegroupElement hpp::pinocchio::LiegroupSpace::element | ( | vectorIn_t | q | ) | const |
Create a LiegroupElement from a configuration.
◆ elementConstRef()
| LiegroupElementConstRef hpp::pinocchio::LiegroupSpace::elementConstRef | ( | vectorIn_t | q | ) | const |
Create a LiegroupElementRef from a configuration.
◆ elementRef()
| LiegroupElementRef hpp::pinocchio::LiegroupSpace::elementRef | ( | vectorOut_t | q | ) | const |
Create a LiegroupElementRef from a configuration.
◆ empty()
|
static |
Return empty Lie group.
◆ exp()
| LiegroupElement hpp::pinocchio::LiegroupSpace::exp | ( | vectorIn_t | v | ) | const |
Return exponential of a tangent vector.
◆ interpolate()
| void hpp::pinocchio::LiegroupSpace::interpolate | ( | vectorIn_t | q0, |
| vectorIn_t | q1, | ||
| value_type | u, | ||
| vectorOut_t | result | ||
| ) | const |
Interpolate between two elements of the Lie group.
This is equivalent to 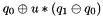 .
.
- Parameters
-
q0,q1 two elements u in [0,1] position along the interpolation: q0 for u=0, q1 for u=1
- Return values
-
result interpolated configuration
◆ isVectorSpace()
| bool hpp::pinocchio::LiegroupSpace::isVectorSpace | ( | ) | const |
◆ Jdifference()
| void hpp::pinocchio::LiegroupSpace::Jdifference | ( | vectorIn_t | q0, |
| vectorIn_t | q1, | ||
| matrixOut_t | J0, | ||
| matrixOut_t | J1 | ||
| ) | const |
- Deprecated:
- Use dDifference_dq0 and dDifference_dq1
◆ liegroupTypes()
|
inline |
Get reference to vector of elementary types.
◆ mergeVectorSpaces()
| void hpp::pinocchio::LiegroupSpace::mergeVectorSpaces | ( | ) |
◆ name()
| std::string hpp::pinocchio::LiegroupSpace::name | ( | ) | const |
Return name of Lie group.
◆ neutral()
| LiegroupElement hpp::pinocchio::LiegroupSpace::neutral | ( | ) | const |
Return the neutral element as a vector.
◆ nq() [1/2]
|
inline |
Dimension of the vector representation.
◆ nq() [2/2]
| size_type hpp::pinocchio::LiegroupSpace::nq | ( | const std::size_t & | rank | ) | const |
Dimension of elementary Liegroup at given rank.
◆ nv() [1/2]
|
inline |
Dimension of the Lie group tangent space.
◆ nv() [2/2]
| size_type hpp::pinocchio::LiegroupSpace::nv | ( | const std::size_t & | rank | ) | const |
Dimension of elementary Liegroup tangent space at given rank.
◆ operator!=()
| bool hpp::pinocchio::LiegroupSpace::operator!= | ( | const LiegroupSpace & | other | ) | const |
◆ operator*=()
| LiegroupSpacePtr_t hpp::pinocchio::LiegroupSpace::operator*= | ( | const LiegroupSpaceConstPtr_t & | other | ) |
◆ operator==()
| bool hpp::pinocchio::LiegroupSpace::operator== | ( | const LiegroupSpace & | other | ) | const |
◆ R1()
|
static |
Return 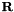 as a Lie group.
as a Lie group.
◆ R2()
|
static |
Return 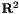 as a Lie group.
as a Lie group.
◆ R2xSO2()
|
static |
Return 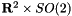 .
.
◆ R3()
|
static |
Return 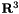 as a Lie group.
as a Lie group.
◆ R3xSO3()
|
static |
Return 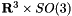 .
.
◆ Rn()
|
static |
Return 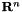 as a Lie group
as a Lie group
- Parameters
-
n dimension of vector space
◆ SE2()
|
static |
Return 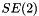 .
.
◆ SE3()
|
static |
Return 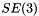 .
.
◆ SO2()
|
static |
Return 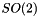 .
.
◆ SO3()
|
static |
Return 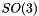 .
.
◆ vectorSpacesMerged()
| LiegroupSpacePtr_t hpp::pinocchio::LiegroupSpace::vectorSpacesMerged | ( | ) | const |
The documentation for this class was generated from the following file:
- include/hpp/pinocchio/liegroup-space.hh
