Configurations of robots, as well as some values like the position of a robot joint with respect to a fixed frame belong to differential manifolds that have the structure of Lie groups. These manifolds are the cartesian products of the following elementary Lie groups
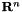 ,
, 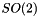 the group of rotations in the plane represented by a vector of dimension 2
the group of rotations in the plane represented by a vector of dimension 2 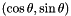 for a rotation of angle
for a rotation of angle 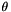 ,
, 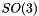 the group of rotations in the 3d space represented by a quaternion
the group of rotations in the 3d space represented by a quaternion 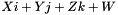 (ie a vector of dimension 4),
(ie a vector of dimension 4), 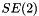 the group of rigid-body motions in the plane, represented by a vector of dimention 4
the group of rigid-body motions in the plane, represented by a vector of dimention 4 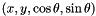 ,
, 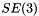 , the group of rigid-body motion in 3d space, represented by a vector of dimension 7
, the group of rigid-body motion in 3d space, represented by a vector of dimension 7 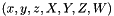 .
.
◆ LiegroupType
Elementary Lie groups A boost variant with the following classes:
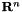 , where
, where 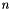 is either 1, 2, 3 or dynamic,
is either 1, 2, 3 or dynamic, 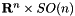 , where
, where 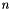 is either 2 or 3,
is either 2 or 3, 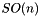 , where
, where 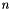 is either 2 or 3,
is either 2 or 3, 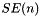 , where
, where 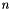 is either 2 or 3.
is either 2 or 3. - See also
- hpp::pinocchio::liegroup::VectorSpaceOperation, hpp::pinocchio::liegroup::CartesianProductOperation, hpp::pinocchio::liegroup::SpecialOrthogonalOperation, hpp::pinocchio::liegroup::SpecialEuclideanOperation,
◆ DerivativeProduct
| Enumerator |
|---|
| DerivativeTimesInput | |
| InputTimesDerivative | |
◆ operator*()
Cartesian product between Lie groups.
◆ operator+()
template<typename vector_type >
Integration of a velocity vector from a configuration
- Parameters
-
| e | element of the Lie group, |
| v | element of the tangent space of the Lie group. |
- Returns
- the element of the Lie group resulting from the integration
By extension of the vector space case, we represent the integration of a constant velocity during unit time by an addition
◆ operator-()
template<typename vector_type1 , typename vector_type2 >
Difference between two configurations
- Parameters
-
| e1,e2 | elements of the Lie group, |
- Returns
- the velocity that integrated from e2 yiels e1
By extension of the vector space case, we represent the integration of a constant velocity during unit time by an addition
◆ operator<<()
| std::ostream& hpp::pinocchio::operator<< |
( |
std::ostream & |
os, |
|
|
const LiegroupSpace & |
space |
|
) |
| |
|
inline |
◆ operator^()
Cartesian power by an integer.
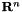 ,
, 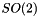 the group of rotations in the plane represented by a vector of dimension 2
the group of rotations in the plane represented by a vector of dimension 2 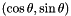 for a rotation of angle
for a rotation of angle 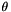 ,
, 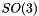 the group of rotations in the 3d space represented by a quaternion
the group of rotations in the 3d space represented by a quaternion 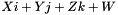 (ie a vector of dimension 4),
(ie a vector of dimension 4), 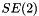 the group of rigid-body motions in the plane, represented by a vector of dimention 4
the group of rigid-body motions in the plane, represented by a vector of dimention 4 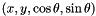 ,
, 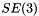 , the group of rigid-body motion in 3d space, represented by a vector of dimension 7
, the group of rigid-body motion in 3d space, represented by a vector of dimension 7 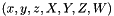 .
. 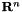 , where
, where 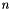 is either 1, 2, 3 or dynamic,
is either 1, 2, 3 or dynamic, 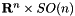 , where
, where 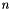 is either 2 or 3,
is either 2 or 3, 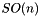 , where
, where 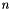 is either 2 or 3,
is either 2 or 3, 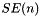 , where
, where 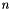 is either 2 or 3.
is either 2 or 3.
